如何通过K折交叉验证大幅降低机器学习核心参数估计偏差？揭秘Chernozhukov的渐近无偏证明

如今，在数据科学领域，降低机器学习算法收敛速度慢对关键参数造成的影响成了一大难题，这个问题涉及诸多值得深入研究的内容。

降低核心参数影响的方法

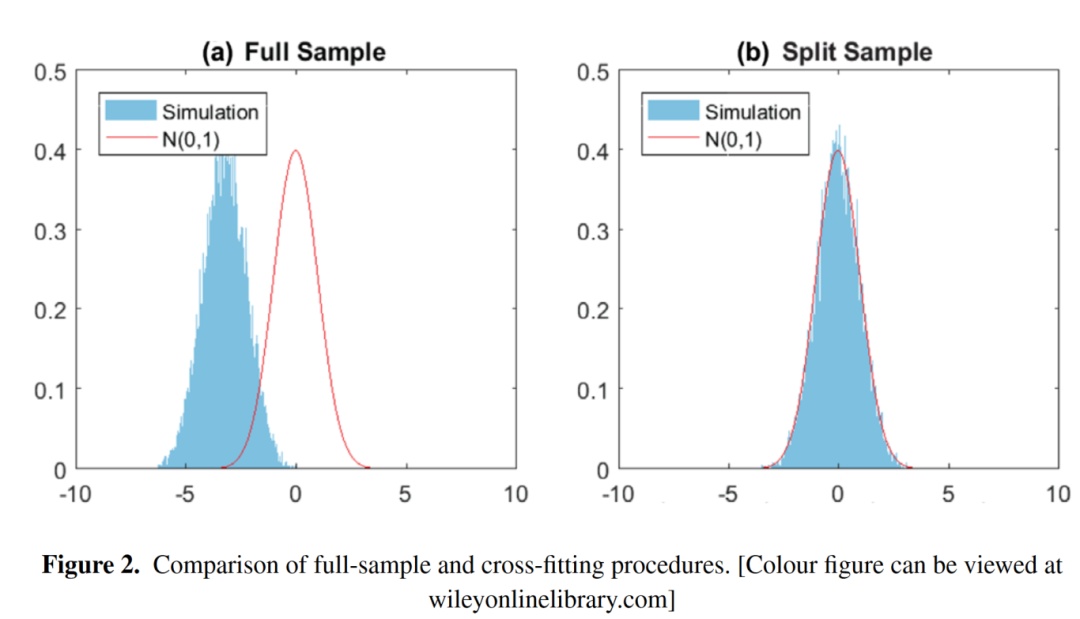
在双重机器学习领域，有一种特别的方法。它将样本随机划分为K组，就好比把苹果按照一定规则分成了K堆。每次，我们剔除一组数据来训练机器学习模型，然后用这个模型来调整核心参数。这个过程要重复K次。这种方式在一定程度上打破了常规，创造了一种新的判断核心参数影响的方法。这种方法适用于那些机器学习算法收敛速度慢且核心参数影响显著的情况，为处理这类问题提供了新的思路。这种做法并非空想，而是基于实践和研究得出的。

理论上讲，这种随机分配样本的方法为数据提供了多种组合途径以供模型学习。这使数据的丰富性在训练过程中得到了强调。同时，各种组合的数据在训练后对关键参数的作用也发生了重新分配。因此，可以有效减少对关键参数估计的误差。

理论支持与证明

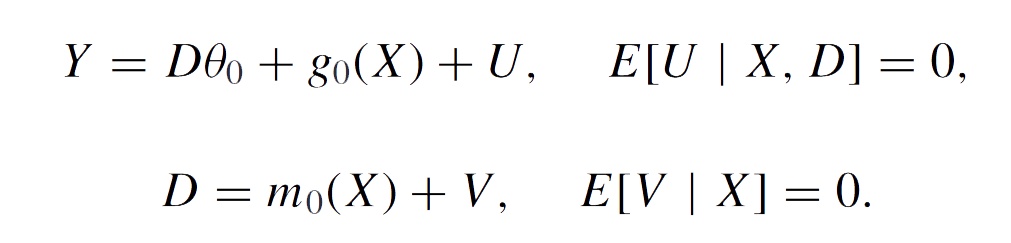
2018年，Chernozhukov等人证实，完成前述两步后，关键参数的估算趋于无偏且呈渐近正态分布。这一理论成果为该方法的正确性与实效性奠定了坚实的理论基础。这就像在黑暗中点亮了一盏灯。有了这一证明，研究人员便可以放心地在相关领域应用这一方法。

它还如同一个衡量准则。凭借它，后续的研究或应用一旦出现误差，便可依据此理论进行调整。这成为该方法拓展至更广范围的通行证。若缺少这一理论作为支撑，其在实际应用中的说服力或许会显著减弱。

部分线性回归模型中的应用

在简单的线性回归模型中，例如与实际生产和日常生活相关的模型，其关键参数是θ0。对于未知的函数或高维的冗余参数，估计核心参数需要遵循明确步骤。首先，需要对数据进行划分，以IIK数据为例，将Y和D分别作为标签，X作为输入，用于训练机器学习模型。简单来说，这就像是在构建一座桥梁，Y和D是桥梁的两端，而X则是中间的支撑结构。

接着，重复上述步骤K次以获得样本外残差，随后，将Y的残差视为因变量，D的残差作为自变量，通过普通最小二乘法进行回归，以估算θ0。这一过程犹如在迷宫中寻找出路，每一步都是通往核心参数的目标路径。这一系列回归操作实现了Neyman正交化，从而使得双重机器学习既具备了Neyman正交化的优势，又享有了交叉拟合的益处。

实际研究案例

2020年，Dube等人在探讨在线劳动市场的劳动供给弹性时，采用了这一方法。在Mturk平台上，雇主发布任务，劳动者按需完成任务以获得报酬。任务时长和报酬与任务内容紧密相连，而变量x则包含众多固定因素。然而，该模型在处理任务难度与报酬关联性问题上存在挑战，且由于x维度众多，直接分析变得较为复杂。

他们采用Doc2Vec和词袋模型来扩展任务标题和描述的文本维度，接着用随机森林拟合部分线性模型，从而获得无偏估计。这一做法将抽象的双重机器学习方法应用于实际场景，就如同将理论公式用于实际工程设计，展示了其在复杂现实中的实用价值。

广泛的应用领域

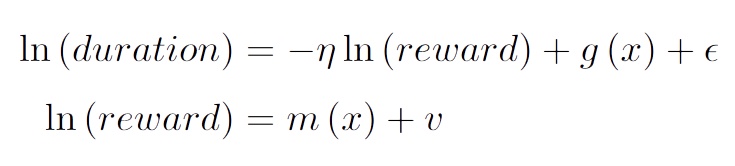
在经济和统计学研究的众多领域中，双重机器学习正逐渐被广泛采用。以因果推断为例，Chernozhukov在2017年采用了一种双向稳健的方法，对无混淆分配假设下的平均处理效应以及处理组平均处理效应的估计问题进行了探讨，并应用了相关技术。在其他经济统计领域，也有各种不同的研究情境，例如在分析消费行为与市场环境的关系时，一旦遇到需要精确估计关键参数的情况，这种方法便能发挥其作用。

每个应用场景都证明了这种方法的有效性。它就像一块块叠加的基石，让这种方法在多个学科中稳固立足。随着应用范围的扩大，该方法也在持续地得到优化和提升。

未来发展展望

尽管双重机器学习已在多个领域得到应用，但仍有广阔的发展前景。比如，面对更复杂的数据结构或不同模型假设，现有模式可能需作调整。在数据量持续膨胀的当下，增长速度的加快或许会引发新的挑战。

新的混合模型能否在双重机器学习的基础上实现创新？又或者，在分析特定行业，比如环保行业碳排放与经济发展关系时，双重机器学习应如何更有效地发挥作用？这些问题都值得我们深入探讨。

你认为双重机器学习今后会有怎样的改进？期待大家积极参与讨论，并给予点赞和转发。