图像去模糊有突破，新方法适用于所有CV二维任务？

图像处理领域里，图像去模糊技术一直备受瞩目，成为热门讨论焦点。而传统方法的不足促使研究者们持续寻找创新解决方案。

传统CNN的局限

传统的卷积神经网络在图像去模糊上存在不少缺陷。比如，在处理监控摄像头捕捉的画面这类实际应用中，它们主要依赖局部操作。这种做法难以全面把握图像信息。因此，面对大面积模糊，它们只能局部改善，效果并不理想。而且，从时间效率来看，基础的局部操作速度较慢，因为需要逐个处理局部区域，无法迅速实现整体去模糊。

面对传统方法在处理空间变化特性上的局限，研究路径亟需调整。图像内容的空间变化往往复杂多变，而传统方法难以有效适应这种复杂性，导致图像去模糊的效果难以达到高效和高质量。

Transformer的潜力与挑战

Transformer模型技术日益进步，成为新的期待。在众多高级视觉任务中，它展现出卓越的全局上下文建模实力。不论是在科研室的测试，还是在工业拍摄场景中的实际应用，其表现都相当出色。

Transformer中的scaled dot-product attention机制存在二次的时空复杂度问题。这个问题必须引起重视。特别是当处理高分辨率图像时，这种复杂度会减慢处理速度，并提升成本。以高端相机拍摄的高分辨率图像为例，在去模糊处理过程中，这种计算复杂度的提升会导致过程变得异常缓慢，同时消耗大量资源。

频域下的解决方案

为了解决这些问题，文章提出了一种基于频域的高效Transformer算法。该方法用元素相乘操作替换了空间域中的矩阵运算，以估算缩放点积注意力。这种改动非常关键。

从理论层面来看，元素乘积操作在简化复杂度方面表现更佳。我们无需执行繁复的矩阵运算，仍能实现相似效果。在具体实验中，众多高分辨率图像在此新法下，处理速度明显加快。这不仅是理论上的突破，更是实际应用中得以证实的成效。

高效的频域自注意力求解器

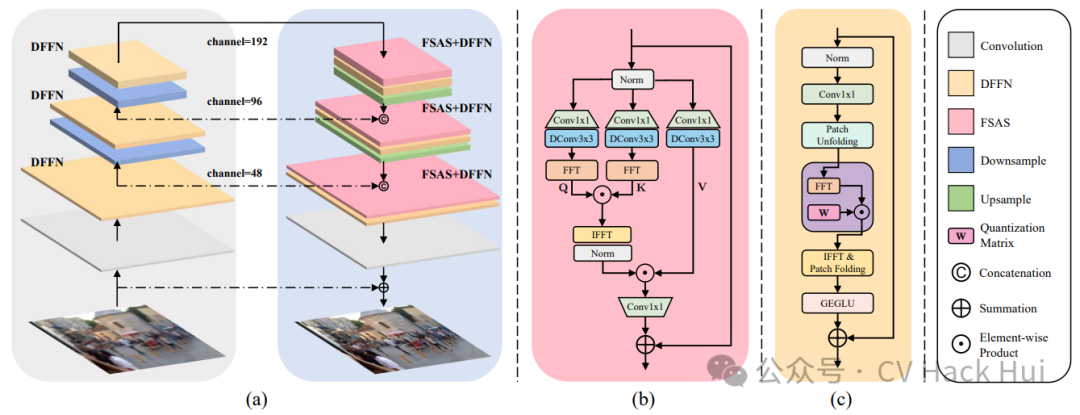
FSAS求解器应运而生。该求解器运用快速傅里叶变换（FFT）在频域内对Fq与Fk的相关性进行估算。这一方法依据卷积定理，即在空间域中进行的卷积操作，在频域中可以转化为逐元素相乘的操作。

FSAS在很多大型图像数据集中表现突出。它显著减少了传统自注意力机制的计算负担。从数据处理的角度看，它在处理大尺寸、高清晰度图像时，大幅降低了计算成本，减轻了噪声干扰。在众多图像编辑软件的应用中，这种改进使得用户在图像去模糊处理时，能够获得更快的速度和更优的质量。

判别性频域前馈网络

提出了判别性频域前馈网络，简称DFFN。此网络借鉴了JPEG压缩技术，并加入了门控功能。设计初衷是为了在恢复图像清晰度时，合理选择保留哪些低频与高频信息。

在实际操作时，不同种类的图像在低频与高频信息上所承载的意义各异。以风景照为例，低频信息通常关联到整体形状，而高频则与细节紧密相连。通过这种有目的的信息保留，图像去模糊的处理效果能更贴合各类图像的特性，从而更有效地还原图像的本来面目。

实验结果展示

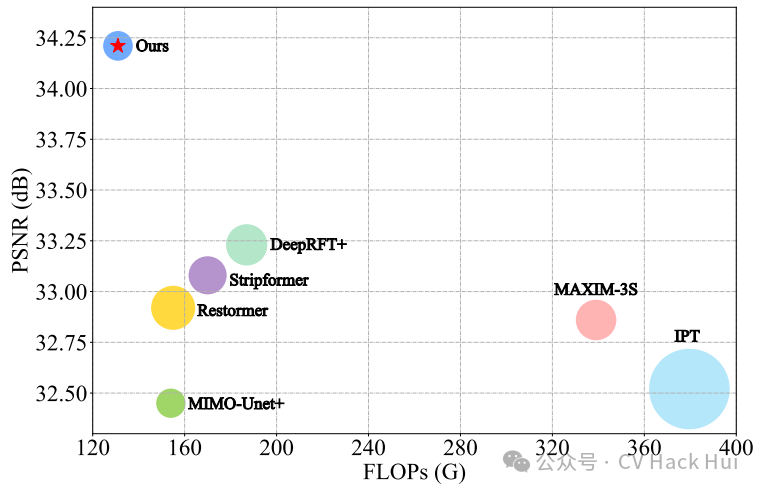
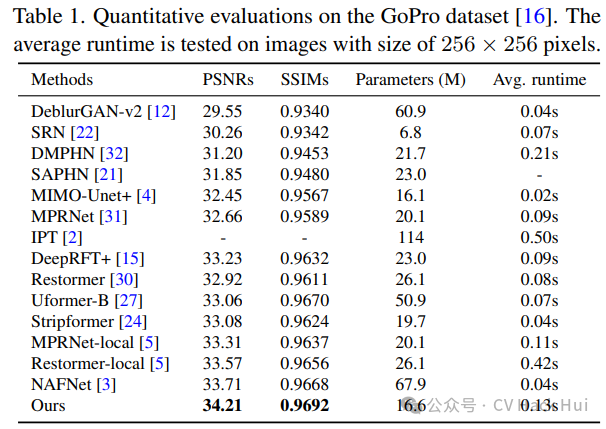
在GoPro数据集上进行了对比测试。结果显示，新方法制作出的去模糊图像，无论是从PSNR（峰值信噪比）还是SSIM（结构相似性）指标来看，都表现更佳。视觉效果同样出色。这表明，结合了FSAS和DFFN的编码器-解码器架构网络是有效的。该方法具有实际应用价值，对图像去模糊技术的实际应用具有积极推动作用。

最后我想请教各位，关于图像去模糊技术，你们认为今后还有哪些途径可以实现更深入的改进？

class FSAS(nn.Module):    def __init__(self, dim, bias=False):        super(FSAS, self).__init__()        self.to_hidden = nn.Conv2d(dim, dim * 6, kernel_size=1, bias=bias)        self.to_hidden_dw = nn.Conv2d(dim * 6, dim * 6, kernel_size=3, stride=1, padding=1, groups=dim * 6, bias=bias)        self.project_out = nn.Conv2d(dim * 2, dim, kernel_size=1, bias=bias)        self.norm = LayerNorm(dim * 2, LayerNorm_type='WithBias')        self.patch_size = 8    def forward(self, x):        hidden = self.to_hidden(x)        q, k, v = self.to_hidden_dw(hidden).chunk(3, dim=1)        q_patch = rearrange(q, 'b c (h patch1) (w patch2) -> b c h w patch1 patch2', patch1=self.patch_size,                            patch2=self.patch_size)        k_patch = rearrange(k, 'b c (h patch1) (w patch2) -> b c h w patch1 patch2', patch1=self.patch_size,                            patch2=self.patch_size)        q_fft = torch.fft.rfft2(q_patch.float())        k_fft = torch.fft.rfft2(k_patch.float())        out = q_fft * k_fft        out = torch.fft.irfft2(out, s=(self.patch_size, self.patch_size))        out = rearrange(out, 'b c h w patch1 patch2 -> b c (h patch1) (w patch2)', patch1=self.patch_size,                        patch2=self.patch_size)        out = self.norm(out)        output = v * out        output = self.project_out(output)        return outputif __name__ == '__main__':    fsas= FSAS(32).to(device)    input = torch.rand(1, 32, 256, 256).to(device)  # 输入张量    output = fsas(input)  # 前向传播    print(f"n输入张量形状: {input.shape}")    print(f"输出张量形状: {output.shape}")